Blackholes but in ASCII (All thanks to Interstellar)

What I learned as well as source for anyone attempting this

While you read this, listen to the film's score, a masterpiece [1]

Black holes are amazing and also intriguing. Which is why, inspired by the rotating donut, I decided to make a black hole rendering purely from ASCII [2] I will be using: '.', ',', '-', '~', ':', ';', '=', '!', '*', '#', '$', '@' . Not in c however, since that is not my forte, but in python. No OpenGL, no graphics library, just pure math and ASCII characters. [3]

TL;DR - Made a code to show a live black hole [4] A curved gravitational field made up of spacetime, where so much matter is condenced in such a small area, that it doesn't technically have any mass. Bonkers ik... in action with only ASCII. Link to code.

What???

I know right, thought so too initially. But below, I will break down the process bit by bit to make it easier to understand. This has taken me deep into a rabbit hole and I would like to share it with you guys.

Why ASCII?

The donut ASCII has always been on the back of my mind, and I recently came upon it while revisiting old memories. I was intrigued by how characters can be placed with simple math to create intricate renderings. As such, my love for Interstellar and coincidental reminder of the donut.c led me to a unified idea: a black hole but in ASCII!

Also, it's cool because after doing a little research, the first image (or visual) was done by a CNRS researcher as early as 1979, and really you will see below how similar my results are with this. Each dot kind of looks like ASCII, but now rotating!

Math

With a simple search one can discover a plethora of black holes, with each having distinct variations. But for the sake of simplicty and my peace of mind we will be working with a black hole popularly represented in Interstellar such as the one below!

Me!

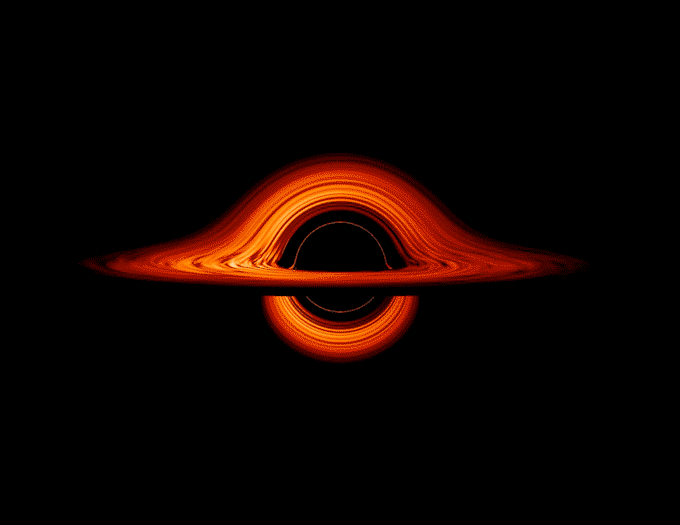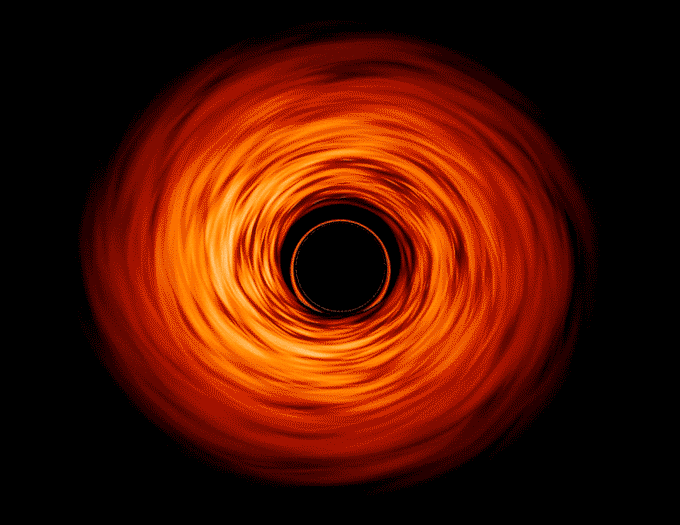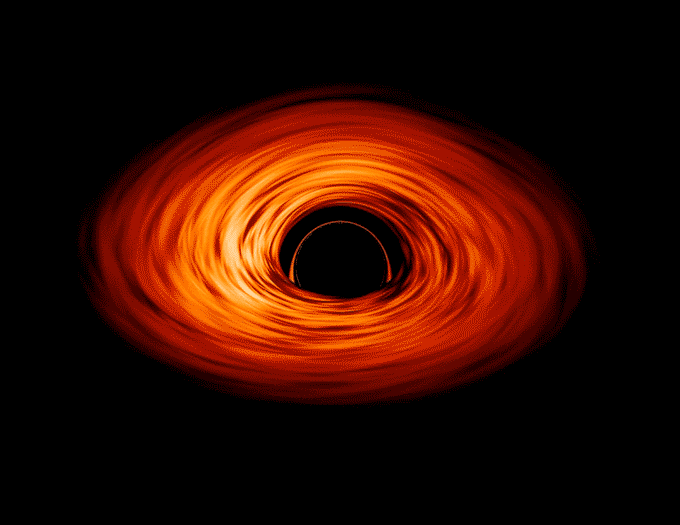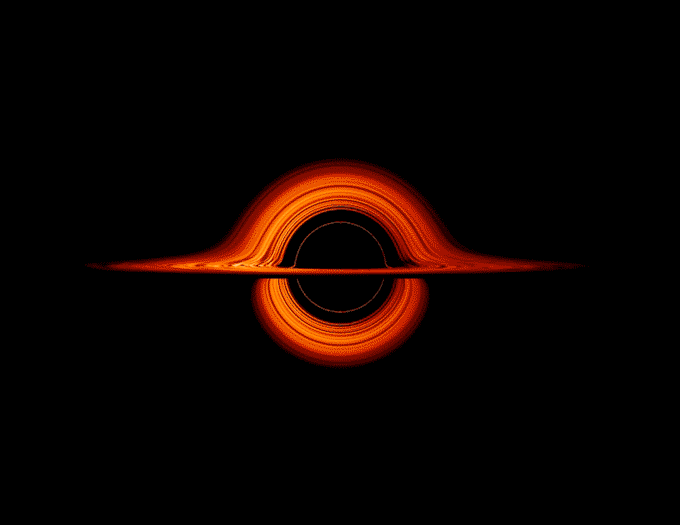
For more information on it's part and a deep scientific jargon, check out the actual experts. Lets get started!

The first step is to understand the math behind a black hole is to use the good ol' desmos. Below you will find the visualizations I pulled from different sourcees to deepen understanding of what this task entails.

Me!
This represents the horizion which is just a sphere. It is going to be going outwards at the speed of light! [5]
Me!
This represents the accretion disc of the black hole. A kind of brain-scrambling representation of the outer part of the black hole! [6]

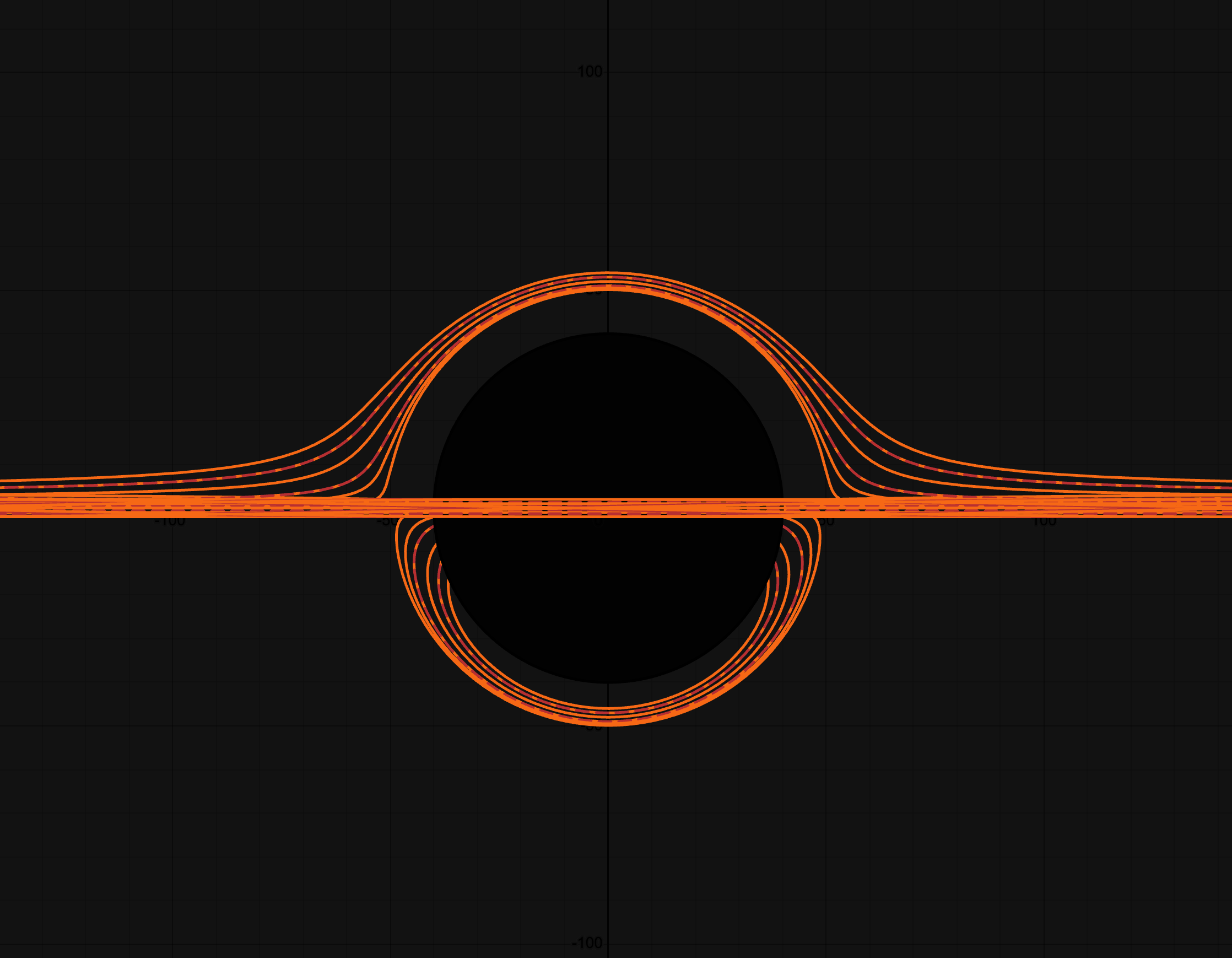
So, let's start with the sphere. Formula is:
x^2 + y^2 + z^2 = r^2

Were we going to make a cube, then it would have been much easier. A cube has 8 points and lines connecting them. It could easily be represented below as all it's points:
points = [(-1, -1, -1), (1, -1, -1), (1, 1, -1), (-1, 1, -1), (-1, -1, 1), (1, -1, 1), (1, 1, 1), (-1, 1, 1)]
But a sphere is different, it has infinite points. So how do we do this? We first select the radius, then we use parametric equations to represent the sphere. The formula for a sphere is:
x = r * sin(φ) * cos(θ)
y = r * sin(φ) * sin(θ)
z = r * cos(φ)
Where φ (phi) is the polar angle (0 to π) and θ (theta) is the azimuthal [7] This is not a mayan demigod, it's a basically an angle around an axis angle (0 to 2π). 


            import math

            r = 0.5 // limiting this to 0.5 for scaling purposes
            points = []
            // Parametric equations
            for phi in [i * math.pi / 20 for i in range(21)]:  # 0 to π
                for theta in [i * 2 * math.pi / 40 for i in range(41)]:  # 0 to 2π
                    x = r * math.sin(phi) * math.cos(theta) // x = r * sin(φ) * cos(θ)
                    y = r * math.sin(phi) * math.sin(theta) // y = r * sin(φ) * sin(θ)
                    z = r * math.cos(phi) // z = r * cos(φ)
                    points.append((x, y, z))